他们，在数学里耍流氓......

zyzme

数学一向以严谨的思维著称，每一步推理都需要严格的理由。但在数学历史中，漏洞百出的数学推理也频频出现。有趣的是，即使是这些不严格的思路也充满着智慧，在数学中的地位不亚于那些伟大的证明。

【1】伽利略

车轮在地上旋转一圈的过程中，车轮圆周上的某一点划过的曲线就叫做“旋轮线”。


在数学和物理中，旋轮线都有着非常重要而优美的性质。
比如说，一段旋轮线下方的面积恰好是这个圆的面积的三倍。这个结论最早是由伽利略（Galileo Galilei，1564-1642）发现的。不过，在没有微积分的时代，计算曲线下方的面积几乎是一件不可能完成的任务。伽利略是如何求出旋轮线下方的面积的呢？

他的方法简单得实在是出人意料：它在金属板上切出旋轮线的形状，拿到秤上称了称，发现重量正好是对应的圆形金属片的三倍。在试遍了各种数学方法却都以失败告终之后，伽利略果断地耍起了流氓，用物理实验的方法测出了图形的面积。

用物理实验解决数学问题也不是一件稀罕事了，广义费马点（generalized Fermat point）问题就能用一套并不复杂的力学系统解出，施泰纳问题（Steiner tree problem）也可以用肥皂膜实验瞬间秒杀。

【2】欧拉

在数学史上，很多漂亮的定理最初的证明都是错误的。最典型的例子可能就是1735 年大数学家欧拉（Euler）的“证明”了。他曾经仔细研究过所有完全平方数的倒数和的极限值，并且给出了一个漂亮的解答：

这是一个出人意料的答案，圆周率 π 毫无征兆地出现在了与几何完全没有关系的场合中。
欧拉的证明另辟蹊径，采用了一种常人完全想不到的绝妙方法。他根据方程 sin(x)/x = 0 的解，对 sin(x)/x 的级数展开进行因式分解，再利用对比系数的方法神奇地得到了问题的答案。不过，利用方程的解进行因式分解的方法只适用于有限多项式，在当时的数学背景下，这种方法不能直接套用到无穷级数上。虽然如此，欧拉利用这种不严格的类比，却得出了正确的结果。

欧拉大师耍了一个漂亮的流氓。

【3】最经典的“无字证明”
一些定理的直观理解虽然毫无逻辑可言，完全算不上是数学证明，但这些精巧而欢乐的视角，依然让数学家们如痴如醉。

1989 年的《美国数学月刊》（American Mathematical Monthly）上有一个貌似非常困难的数学问题：下图是由一个个小三角形组成的正六边形棋盘，现在请你用右边的三种（仅朝向不同的）菱形把整个棋盘全部摆满（图中只摆了其中一部分），证明当你摆满整个棋盘后，你所使用的每种菱形数量一定相同。

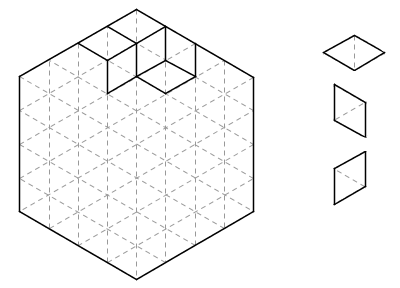
文章末尾提供了一个非常帅的“证明”。
在数学中，类似的流氓证明数不胜数，不过这个可能算是最经典的了。

游客，本帖隐藏的内容需要积分高于 100 才可浏览，您当前积分为 0