|
|
本帖最后由 低沉的游鱼 于 2014-6-17 22:26 编辑
已被APIO题完虐,8分滚粗了。。于是我要下定决心好好学习。首先就学了一下manacher算法,T1要用到的算法
比如一个字符串abacaba,要求出里面所有的回文串。 如果回文串长度是奇数,就直接从中心向两边展开就行了。但如果是偶数呢?我们需要一个对这个字符串稍作变形。将这个字符串变为#a#b#a#c#a#b#a#。(#是一个辅助字符,要保证它在原串里不出现)。这样一来,原来长度是奇数的回文串长度还是奇数,长度为偶数的回文串就变成从其中一个#号展开。我们用p表示在这个新的字符串str中,以str为中心的最长回文串半径。这样一来,p-1表示的以str为中心的回文串在原串中的长度(很好证明,这里不多说)。
先贴一个完整的代码
- #include<iostream>
- #include<cstring>
- using namespace std;
-
- int manacher (char* s, int len)
- {
- int nlen = 2 * len + 3;
- char* str = new char[nlen];
- int i = 0;
- int max = 0;
- str[0] = ' ~';
- str[1] = '#';
- for (; i < len; i++)
- {
- str[i * 2 + 2] = s[i];
- str[i * 2 + 3] = '#';
- }
- str[nlen - 1] = 0;
- int* p = new int[nlen];
-
- for (int i = 1; i < nlen; i++)
- {
- p[i] = 0;
- }
-
- int id = 0;
- for (i = 1; i < nlen; i++)
- {
- if (max > i)
- p[i] = min(p[2*id-i], max-i);
- else
- p[i] = 1;
- while (str[i+p[i]] == str[i-p[i]])
- p[i]++;
- if (p[i]+i > max)
- {
- max = p[i] + i;
- id = i;
- }
- }
-
- int mx = 0;
- for (i = 1; i < nlen; i++)
- {
- if (mx < p[i] - 1)
- mx = p[i] - 1;
- }
- return mx;
- }
-
- int main()
- {
- char ch[100];
- while (cin >> ch)
- {
- cout << manacher(ch, strlen(ch)) << endl;
- }
- return 0;
- }
这一句
if (max > i)
p = min(p[2*id-i], max-i);
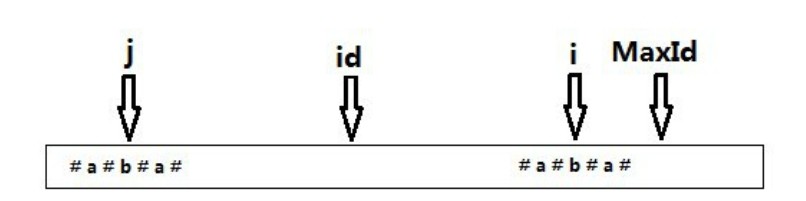
是整个算法中很重要的一个环节,利用了回文串的对称性,避免了许多不必要的计算。max表示的是之前的回文串匹配到的最远的位置,id保存的是这个回文串的i值。p[2*id-i]表示的就是i关于id对称的j的位置。但如果j的回文串长度较长,对称过来以后超出max的话,超出部分是还没有匹配的。因此,应该取的是两者之间较小值。
下图可能有助于理解
 |
|